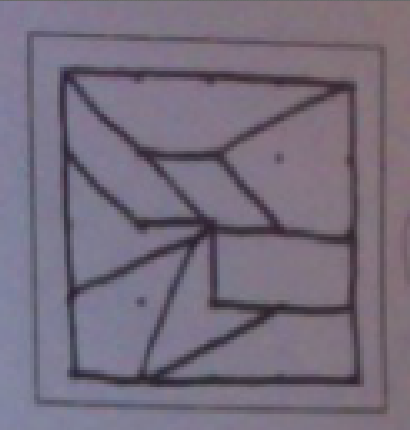
For the past couple of classes we've been talking about quadrilaterals. There are 11 different main types of quadrilaterals we discussed in class, as shown below. For SBG #2 question #7, it said to divide up a Geoboard into four or more different types of quadrilaterals. I not only took this as a challenge to fit as many quadrilaterals as possible on the Geoboard, I challenged myself to represent as many different shapes as possible. These were some of my attempts to fit as many different quadrilaterals onto one Geoboard as possible.
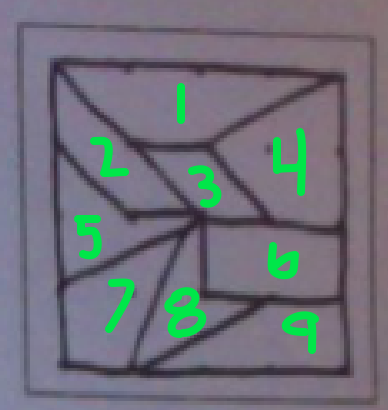
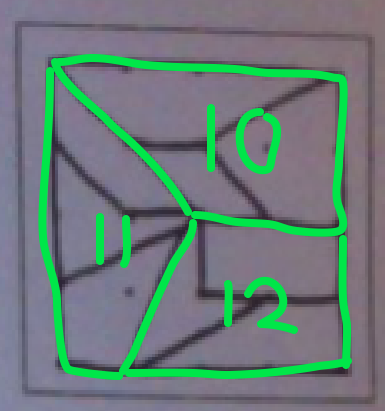
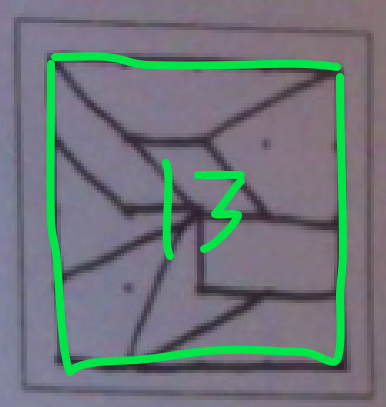
In the end, this was the division I was the most confident in. It is divided up into 9 separate quadrilaterals, which is the most I could fit on one without repeating any of the shapes. Here we have 13 found quadrilaterals, as identified with numbers. At first it only appears to have 9, but a second glance shows there are more quadrilaterals on the Geoboard. This involves combining some of the smaller quadrilaterals to form larger ones. | | The quadrilaterals represented are:
In the original 9:
1. irregular trapezoid
2. regular trapezoid
3. parallelogram
4. general quadrilateral (convex)
5. general concave
6. rectangle
7. kite
8. chevron
9. right trapezoid The others:
10. right trapezoid
11. general quadrilateral
12. right trapezoid
13. square
|
This is similar to the old chess board trick. Someone will ask, "How many squares are on a chess board?" And a person will generally count them up, counting 64 total. But they forget to count all of the combinations of squares that make larger squares! I found a website on this, giving ideas of how to use this principle in the classroom. Looks like it could be useful! Here is the website. http://www.teachingideas.co.uk/maths/chess.htm | |
Reflection: This activity had me thinking about quadrilaterals for a longer time than I wanted to. Trying to divide up the Geoboards into as many quadrilaterals as possible, without repeating any, was frustrating. There were many more trials and errors than what was even shown on the two worksheets. Lots of erasing lines and redrawing them, I wasn't going to settle for there being spaces left over or just putting in a big shape where smaller ones could fit! Over all I enjoyed this. It was fun to explore the different combinations and figure out which shapes fit together best, whether it was smarter to put the points toward the middle or the corners, etc. I learned a lot about quadrilaterals and I don't think it will be easy for me to forget the different types ever again! Also I realized how much teaching potential there was for this. Lots of lesson plan possibilities to be centered around quadrilaterals.
Also, because I spent to much extra time on this, it was the weekly work for both 7 and 8. I would also like for this one to be considered for the SBG grade...because the question came straight from it!
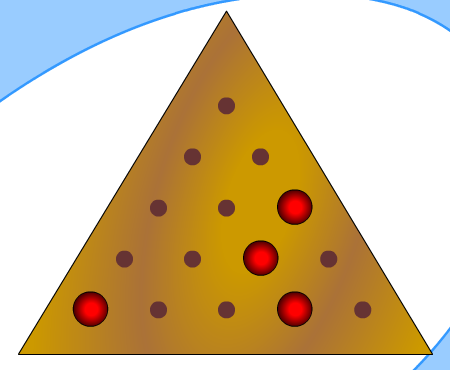
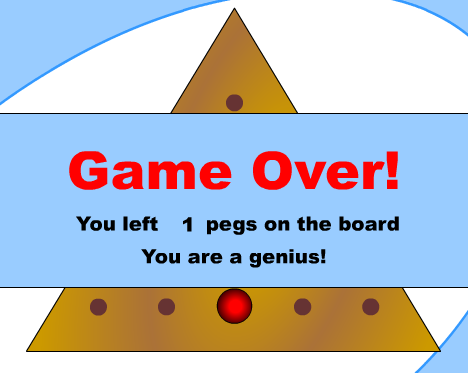
THE CRACKER BARREL TRIANGLE GAME Anyone who has been to Cracker Barrel will recognize this game. My family stops at Cracker Barrel once a year on our annual trip down to Florida for spring break. My older brother and I have this ongoing competition to see who can get down to only one piece on the board. He's a super competitive engineering math guy, so he always tends to win. At everything. And in this case, it usually ends with me having to eat something gross. But the more I thought about this game, I started to wonder if there is some kind of pattern to go with finishing it down to one piece every time. I started to experiment with the game to see if I could find a pattern that would guarantee a win every time. Because I do not have one of these games in my possession, I found an online version to play around with. You can find that version here: http://www.memory-improvement-tips.com/pegs.htmlThe instructions for the game are as follows: After a lot of experimenting, I finally figured out a pattern that worked. This pattern starts with the top hole empty. (It can be any of the corners, just depends on which way you turn the triangle). When I reference the numbers, I am numbering the holes from top-down. Like this: The first 3 jumps to the pattern are: 4-1, 6-4 and 1-6.
The next moves: 7-2, 13-4 and 2-7.
Next: 10-8 and 7-9 clear the second row
15-13 and 12-14 clears the bottom
Now for the last step: 6-13, 14-12 and 11-13. WINNER!
Note that this pattern is only made through an hour or so of trial and error. I played the game multiple times, each time recording my moves. Many times it ended in failure, with multiple pegs left on the board. This pattern was a success. It is proven to work every time that the game is started with the first hole left empty.
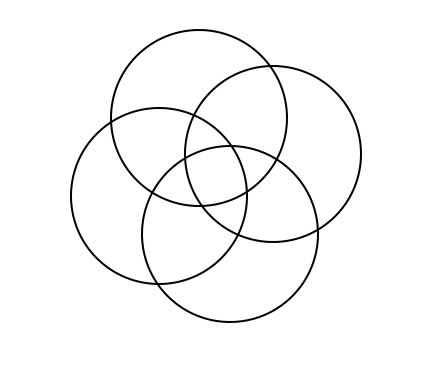
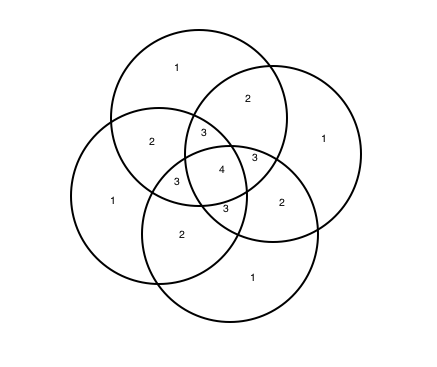
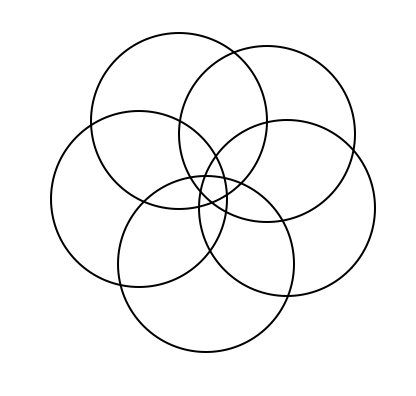
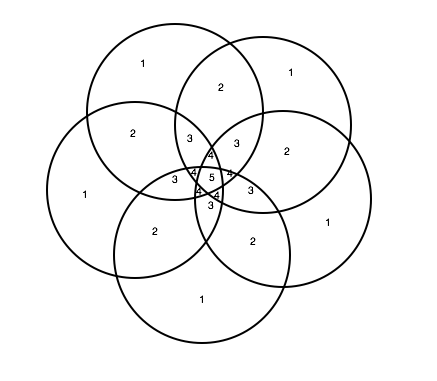
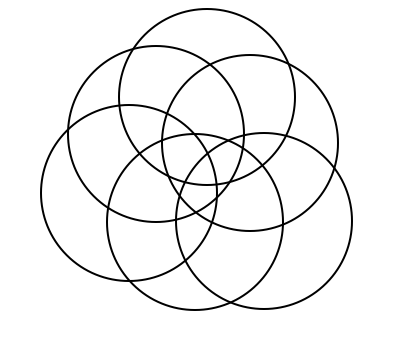
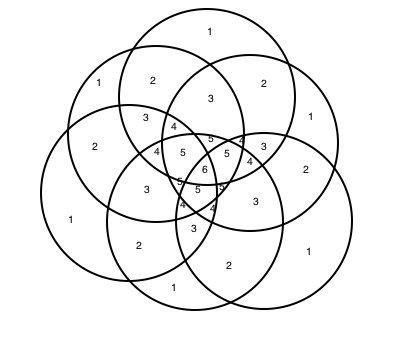
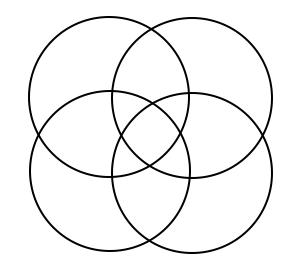
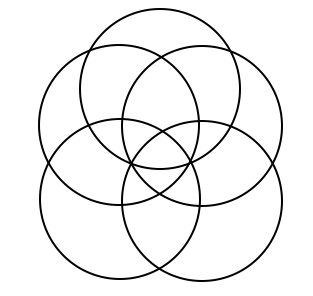
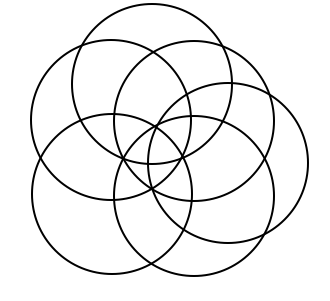
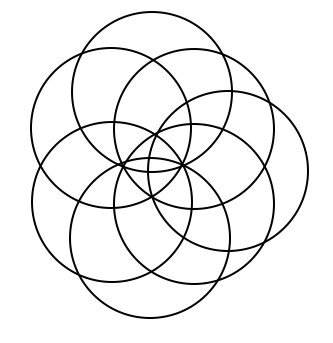
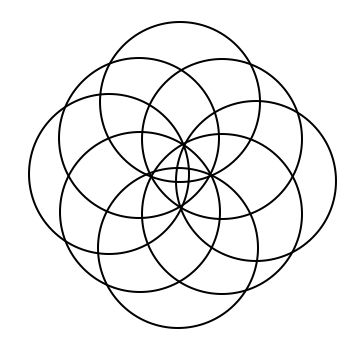
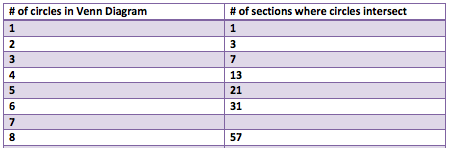
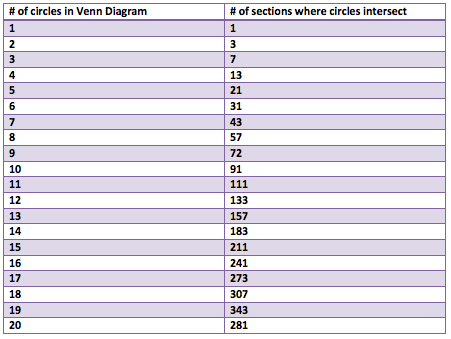
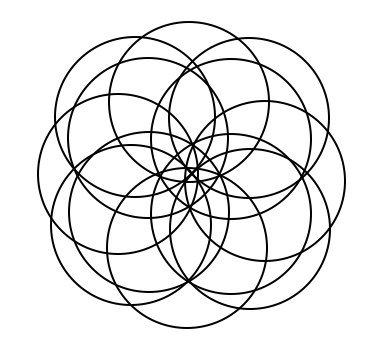
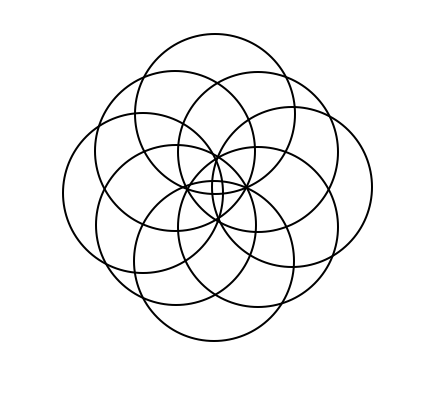
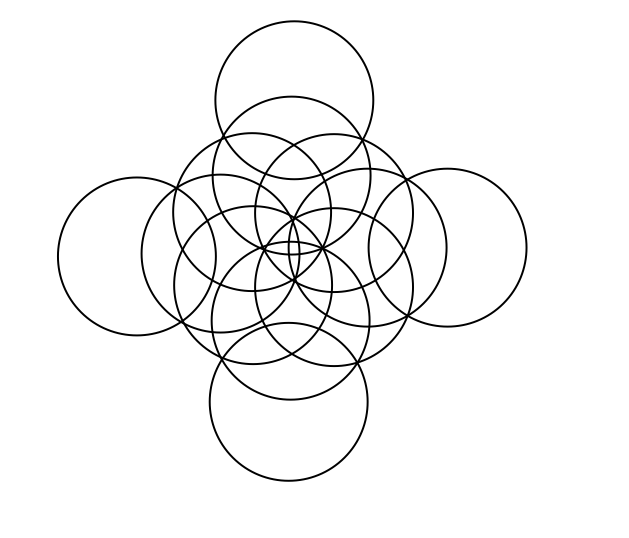
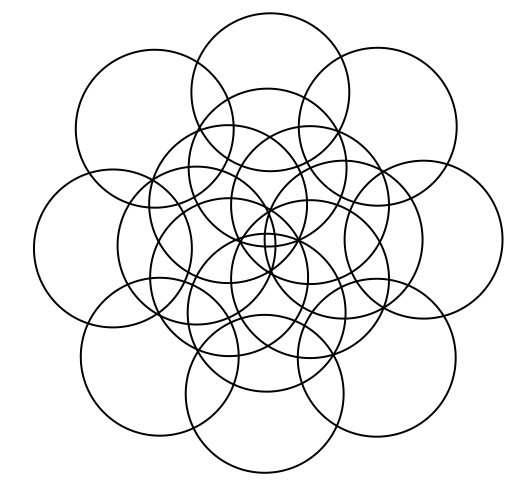
This is a continuation off of something I did for a daily work earlier this past week. For some reason, Venn Diagrams really interest me. It is cool to me how each time you add in a circle, it changes the shape of it entirely. I put together some examples of what a Venn Diagram looks like with 4, 5, 6, and 8 circles. Here's what I came up with. 4 5 6 What I found to be very interesting about this is that working from the outside in, there is a pattern to the number that represents the number of circles that share any given space. For example, on this Venn Diagram for 6 above, there are six spots around the outside that I put a number 1 into. This is because there is only one circle that the space is being owned by. The next level in are the spots being shared by 2 separate circles, the space they intersect. So I put a number 2 in those spots. And so on and so forth throughout the rest of the diagram, I labelled the number of circles that shared the spot. Here you will see a progression of how I created a venn diagram with 8 circles. As you can see, I started with a venn diagram of 4 circles as seen before. I then proceeded to add one circle to each side of the already made venn diagram. I ended up with eight circles total, all converging in the center. Then I started to look at the patterns in the number of sections created each time a circle is added. (As a little bit of a disclaimer, this table only proves to be true when the circles are arranged in a way that correctly follows the pattern, not when circles are randomly added on the sides.) Looking back to the venn diagrams of 4, 5, 6, and the finished product for 8, I counted the number of sections in the diagram. Then I came up with an equation that correlated with the pattern found from the table. So the equation is n(n-1)+1. Using this equation, I was able to fill in the rest of the table. As I was filling in the table, I realized that there was another pattern to what I was doing. I reworked the equation, and found that another equation that works for the same pattern is n^2-(n-1). Tricky stuff! Reflection: I found it interesting that after all of the work I did, I realized another equation that did the exact same job just in a different way. It really was neither shorter or longer, but it provided the same results. Also, I realized about halfway through that the rules I was making and the work I was doing only applied in situations where the circles were placed in a certain way. These rules would not work if the circles are not placed in a way that they are connecting to all of the rest at the center. Over all, this was fun to play around with and figure out. I liked having the chance to realize all of these things, and find this equation, just to satisfy my curiosity instead of doing it because it was a problem on a worksheet that I had to answer.
A few more random experimental patterns I made. Note that these do not follow the rule requirements because they do not all touch the center. However, they all do involve the circles being added in a specific pattern. If the fill tool had not been taken out of Skitch, I would have been able to make some cool designs by adding color to these patterns. Gotta hate that Skitch 2.0 update! Also, I wonder what would happen if the circles were different sizes....
During our first week of class, we talked a lot about patterns. I decided to look into the different types of patterns that exist. When I looked up "different types of patterns" on the internet, I found an entire glossary of definitions for patterns of all sorts. But I decided then to focus on patterns that I would want to teach about in the classroom, and I started making a lesson plan of sorts. I haven't made many of these, so I have no idea if this lesson would be stretched over multiple days or just a single lesson.
Two easy patterns to focus on are repeating patterns and growing patterns.
Pattern — a set of recurring events or objects
Repeating pattern — a type of pattern in which elements repeat in a simple manner (ex. boy, girl, boy, girl, boy, girl)
Growing pattern — a type of pattern in which successive elements grow according to a rule
(ex. 1, 2, 4, 7, 11, 16…)
1. Finding Patterns
I'd begin the lesson by having the students pick out patterns in the room—floor or ceiling tiles,
wallpaper, or clothing, for example. I'd then ask students:
...explain what a pattern is and what it is not.
...what other patterns are always present in our lives? [days in a week, months in a year, the seasons]
2. Making Patterns
Then we'd jump into the next section... making patterns! I'd ask a few students to come up to the front, line up in a row, and have the whole class try to make patterns with the students standing in the line. They might pick out physical characteristics (long hair, short hair, long hair, short hair; boy, girl, boy, girl) or movement (standing, sitting, standing, sitting). Then the students would be split up into groups and asked to create a simple pattern on their own with the people in their group. Each group would be given an area of the room to work with in order to generate their own creative “people patterns.” These would be presented in front of the class after the groups have time to make the patterns.
3. Color and Shape Patterns
The real meat and potatoes starts here...this is where we get the students really thinking critically about patterns. I would draw two patterns on the board or put them up on an overhead screen, and have the students try to predict what would come next in the pattern. The patterns might look something like this...
Then I would show them a growing pattern, like this. I'd explain that the first two color patterns they saw, and (probably) all of the people patterns they made are called repeating patterns. Pattern #3 is a new type of pattern, called a growing pattern.
4. Number Patterns
Next I would introduce number patterns. Instead of using colored dots, I would exchange those for numbers and have them see those as patterns.
For example, here are some repeating number patterns:
1, 2, 1, 2, 1, 2, 1, 2...
1, 3, 3, 1, 3, 3, 1, 3, 3, 1…
And some growing number patterns:
1, 2, 4, 7, 11 ,16, 22…
1, 1, 2, 6, 24, 120, 720…
Students can create their own growing patterns and switch with a partner to figure out what
numbers come next.
Reflection:
I think that this lesson would work well, and starting off with a way to make patterns that uses their bodies would help to make the lesson fun. What I am not so sure about is how long each of these things would take. I would love to do them all in a row, because they progress, but it seems after going through that it would be more of one lesson per day progression. It might not work as is because of time constraints. I think that this would be a good way to ease students into finding patterns with numbers as well.
|








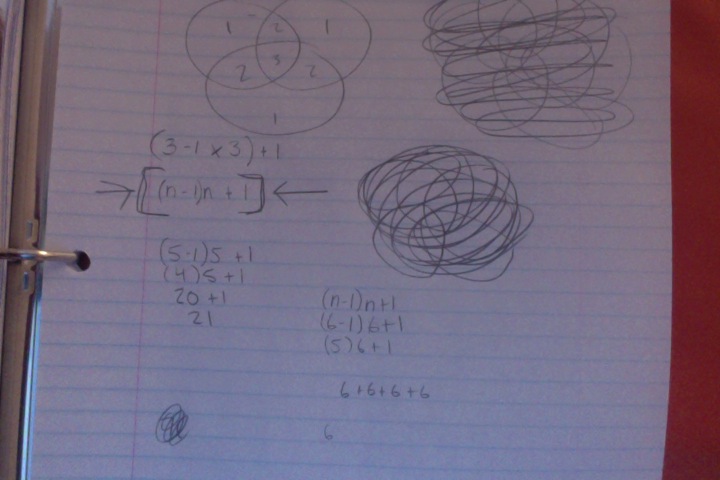



 RSS Feed
RSS Feed