In class this week we talked about the Family Math Night we are doing at a local elementary school in a few weeks. As students we are going to prepare games for this night, and families from the community are going to come to the school for a type of "math carnival" and come to play the games we are preparing for them. My partner and I are currently deciding on a game, and we are hoping to do something with shapes. I'm sure there is something we can do with shapes that will be good for all potential ages, or that we can modify so that it will suit the needs of each age group and be fun for multiple ages!
I'm excited for this math game night. I love having the chance to actually interact with students. So much of the time it seems like we're not given the chance to interact with students until later on in our degrees, once we start student teaching, but I feel that it is important to know what we're getting in to now and get as much experience in classrooms as possible before we get further into our majors.
For the past couple of classes we've been talking about quadrilaterals. There are 11 different main types of quadrilaterals we discussed in class, as shown below.
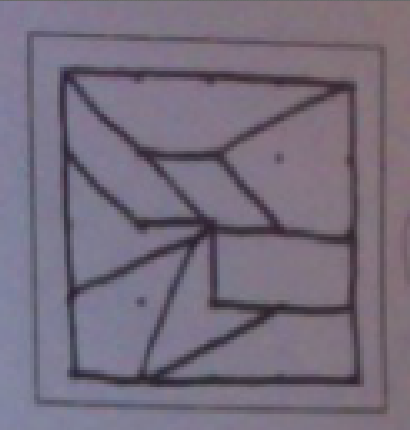
For SBG #2 question #7, it said to divide up a Geoboard into four or more different types of quadrilaterals. I not only took this as a challenge to fit as many quadrilaterals as possible on the Geoboard, I challenged myself to represent as many different shapes as possible. These were some of my attempts to fit as many different quadrilaterals onto one Geoboard as possible.
In the end, this was the division I was the most confident in. It is divided up into 9 separate quadrilaterals, which is the most I could fit on one without repeating any of the shapes.
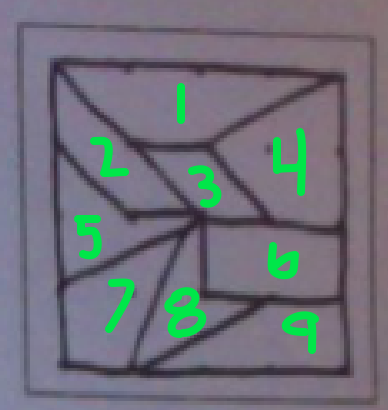
Here we have 13 found quadrilaterals, as identified with numbers. At first it only appears to have 9, but a second glance shows there are more quadrilaterals on the Geoboard. This involves combining some of the smaller quadrilaterals to form larger ones.
| | The quadrilaterals represented are:
In the original 9:
1. irregular trapezoid
2. regular trapezoid
3. parallelogram
4. general quadrilateral (convex)
5. general concave
6. rectangle
7. kite
8. chevron
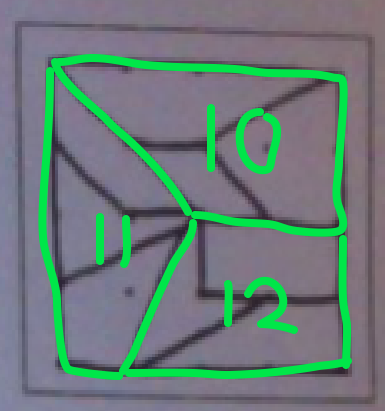
9. right trapezoid The others:
10. right trapezoid
11. general quadrilateral
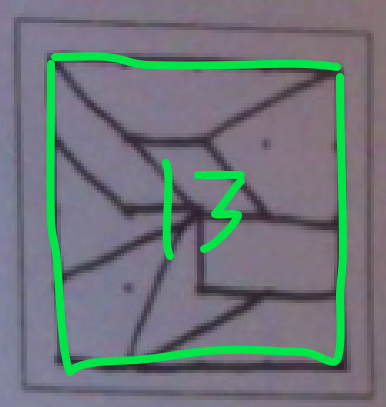
12. right trapezoid
13. square
|
This is similar to the old chess board trick. Someone will ask, "How many squares are on a chess board?" And a person will generally count them up, counting 64 total. But they forget to count all of the combinations of squares that make larger squares! I found a website on this, giving ideas of how to use this principle in the classroom. Looks like it could be useful! Here is the website. http://www.teachingideas.co.uk/maths/chess.htm | |
Reflection: This activity had me thinking about quadrilaterals for a longer time than I wanted to. Trying to divide up the Geoboards into as many quadrilaterals as possible, without repeating any, was frustrating. There were many more trials and errors than what was even shown on the two worksheets. Lots of erasing lines and redrawing them, I wasn't going to settle for there being spaces left over or just putting in a big shape where smaller ones could fit! Over all I enjoyed this. It was fun to explore the different combinations and figure out which shapes fit together best, whether it was smarter to put the points toward the middle or the corners, etc. I learned a lot about quadrilaterals and I don't think it will be easy for me to forget the different types ever again! Also I realized how much teaching potential there was for this. Lots of lesson plan possibilities to be centered around quadrilaterals.
Also, because I spent to much extra time on this, it was the weekly work for both 7 and 8. I would also like for this one to be considered for the SBG grade...because the question came straight from it!
These were the examples from the blog post. At first glance, this makes total sense. It could really confuse a bunch of elementary students!
But further looking at this, you begin to realize that these are some of the very few instances where this applies. Obviously, the fraction has to have the same number in the two diagonals (in the case of the first one, both 9s were the ones that could be cancelled out). In fact, through all of my attempts I have not found any other numbers that it works for. But it is amusing to think that someone would probably take this and just believe it based on a few examples. Doesn't work every time, folks! Don't believe everything you see on the internet.





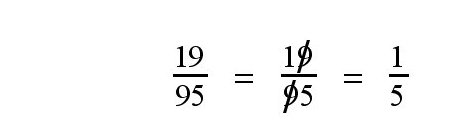
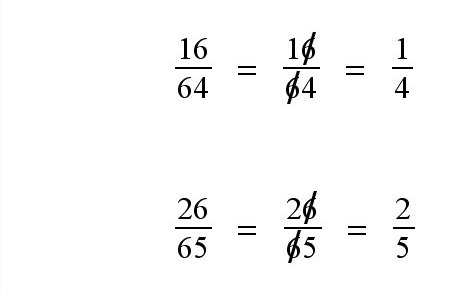
 RSS Feed
RSS Feed