In class on Friday we extended our lesson from the previous Wednesday when we played with dominoes. We learned that dominoes are actually part of a bigger family, called polyominoes. A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. This includes dominoes, trominoes, tetrominoes, pentominoes, hexominoes, and so on. On Friday we worked on making all of the different possible combinations we could come up with for pentominoes, and we found that there are 12 of them total, not counting rotations or flips.
After class, I decided to take on the challenge of finding all of the possibilities for hexominoes (Think dominoes, but with 6 blocks). I wanted to figure out if there was some type of pattern or equation to help figure out how many possibilities of combinations there are for any given number of blocks.
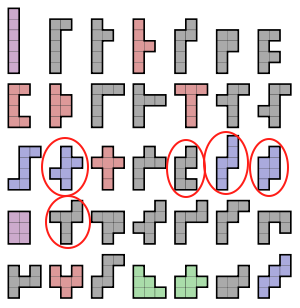
I just started to cut out all of the possible combinations of 6 blocks that I could think of. I found 30 different shapes, and could not find any more. These are the 30 that I cut out.
After class, I decided to take on the challenge of finding all of the possibilities for hexominoes (Think dominoes, but with 6 blocks). I wanted to figure out if there was some type of pattern or equation to help figure out how many possibilities of combinations there are for any given number of blocks.
I just started to cut out all of the possible combinations of 6 blocks that I could think of. I found 30 different shapes, and could not find any more. These are the 30 that I cut out.
Not bad, right? But when I did a search on the internet, a Wikipedia page showed a diagram of all of the potential possibilities for hexominoes. Apparently there are 35 total...I was only missing 5!
I went through and checked off the ones that I had.
So these were the five that I missed.
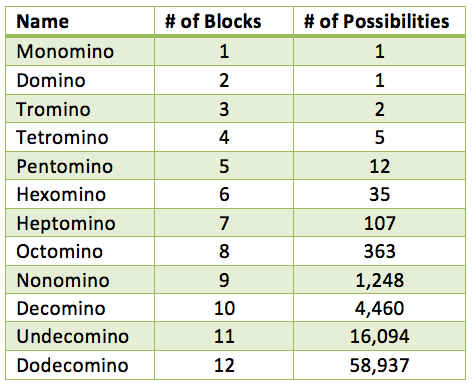
Like I said, not bad. But I still didn't know if there was any rhyme or reason to the number of shapes you could make. Thanks to Wikipedia again, I found out that there has been no formula found that can accurately predict this. However, I created this table based on the information I found. Very interesting!
All in all, this was an interesting experiment. It was surprising to find out that there were more possibilities for the hexominoes than I had been able to find. That is why had originally I decided to explore the question we talked about in class, "how do you know when you have them all?" My answer to that question, I now realize, is that there was no real way for me to know for sure. The only thing I could compare it to was the work of others who have tried it before. I figured that since this was a math-type problem, it would naturally have a formula to help calculate it for n or something. But apparently not all math problems come with perfect formulas! Over all, this was a fun thing to try and figure out. I would love to use these ideas in a classroom someday.
Oh, and here is the link to the Wikipedia page. Better give credit where it is due!
http://en.wikipedia.org/wiki/Polyomino
Oh, and here is the link to the Wikipedia page. Better give credit where it is due!
http://en.wikipedia.org/wiki/Polyomino
RSS Feed